Eur. Phys. J. E (2020) 43: 71
https://doi.org/10.1140/epje/i2020-11999-x

Regular Article

Fluctuating viscoelasticity based on a finite number of dumbbells

¹ Eindhoven University of Technology, Department of Mechanical Engineering, Polymer Technology, PO Box 513, NL-5600 MB, Eindhoven, The Netherlands
² Georgetown University, Department of Physics, Institute for Soft Matter Synthesis and Metrology, 37th and O Streets, 20057, Washington, D.C., N.W., USA
³ School of Mathematics, University of Leeds, LS2 9JT, Leeds, UK

^* e-mail: m.huetter@tue.nl
^** e-mail: peter.olmsted@georgetown.edu
^*** e-mail: d.j.read@leeds.ac.uk

Received: 12 June 2020
Accepted: 2 November 2020
Published online: 20 November 2020

Abstract

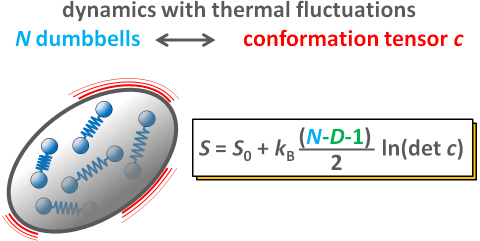
Two alternative routes are taken to derive, on the basis of the dynamics of a finite number of dumbbells, viscoelasticity in terms of a conformation tensor with fluctuations. The first route is a direct approach using stochastic calculus only, and it serves as a benchmark for the second route, which is guided by thermodynamic principles. In the latter, the Helmholtz free energy and a generalized relaxation tensor play a key role. It is shown that the results of the two routes agree only if a finite-size contribution to the Helmholtz free energy of the conformation tensor is taken into account. Using statistical mechanics, this finite-size contribution is derived explicitly in this paper for a large class of models; this contribution is non-zero whenever the number of dumbbells in the volume of observation is finite. It is noted that the generalized relaxation tensor for the conformation tensor does not need any finite-size correction.