Eur. Phys. J. E (2020) 43: 72
https://doi.org/10.1140/epje/i2020-11995-2

Regular Article

Vibrational density of states of amorphous solids with long-ranged power-law-correlated disorder in elasticity

¹ Cavendish Laboratory, University of Cambridge, JJ Thomson Avenue, CB3 0HE, Cambridge, UK
² Department of Physics “A. Pontremoli”, University of Milan, via Celoria 16, 20133, Milano, Italy
³ Statistical Physics Group, Department of Chemical Engineering and Biotechnology, University of Cambridge, Philippa Fawcett Drive, CB3 0AS, Cambridge, UK

^b alessio.zaccone@unimi.it

Received: 25 September 2020
Accepted: 2 November 2020
Published online: 23 November 2020

Abstract

A theory of vibrational excitations based on power-law spatial correlations in the elastic constants (or equivalently in the internal stress) is derived, in order to determine the vibrational density of states D(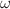$\omega$) of disordered solids. The results provide the first prediction of a boson peak in amorphous materials where spatial correlations in the internal stresses (or elastic constants) are of power-law form, as is often the case in experimental systems, leading to a logarithmic enhancement of (Rayleigh) phonon attenuation. A logarithmic correction of the form 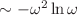$\sim -{\omega }^{2}ln\omega$ is predicted to occur in the plot of the reduced excess DOS for frequencies around the boson peak in 3D. Moreover, the theory provides scaling laws of the density of states in the low-frequency region, including a $\sim {\omega }^4$ regime in 3D, and provides information about how the boson peak intensity depends on the strength of power-law decay of fluctuations in elastic constants or internal stress. Analytical expressions are also derived for the dynamic structure factor for longitudinal excitations, which include a logarithmic correction factor, and numerical calculations are presented supporting the assumptions used in the theory.