https://doi.org/10.1140/epje/i2019-11765-3
Regular Article
Conformational statistics of randomly branching double-folded ring polymers
1
Sissa (Scuola Internazionale Superiore di Studi Avanzati), Via Bonomea 265, 34136, Trieste, Italy
2
Univ Lyon, ENS de Lyon, Univ Claude Bernard, CNRS, Laboratoire de Physique and Centre Blaise Pascal, F-69342, Lyon, France
* e-mail: anrosa@sissa.it
** e-mail: ralf.everaers@ens-lyon.fr
Received:
21
August
2018
Accepted:
13
December
2018
Published online:
21
January
2019
The conformations of topologically constrained double-folded ring polymers can be described as wrappings of randomly branched primitive trees. We extend previous work on the tree statistics under different (solvent) conditions to explore the conformational statistics of double-folded rings in the limit of tight wrapping. In particular, we relate the exponents characterizing the ring statistics to those describing the primitive trees and discuss the distribution functions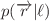 
and 
for the spatial distance,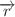 
, and tree contour distance, L, between monomers as a function of their ring contour distance, 
.
Key words: Soft Matter: Polymers and Polyelectrolytes
© EDP Sciences, SIF, Springer-Verlag GmbH Germany, part of Springer Nature, 2019
