Eur. Phys. J. E 34, 20 (2011)
https://doi.org/10.1140/epje/i2011-11020-1

Counter-ions at charged walls: Two-dimensional systems

Laboratoire de Physique Théorique et Modèles Statistiques, Université Paris-Sud, UMR CNRS 8626, 91405, Orsay, France

trizac@lptms.u-psud.fr

Received: 22 November 2010
Accepted: 24 January 2011
Published online: 28 February 2011

Abstract

We study equilibrium statistical mechanics of classical point counter-ions, formulated on 2D Euclidean space with logarithmic Coulomb interactions (infinite number of particles) or on the cylinder surface (finite particle numbers), in the vicinity of a single uniformly charged line (one single double layer), or between two such lines (interacting double layers). The weak-coupling Poisson-Boltzmann theory, which applies when the coupling constant 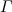is small, is briefly recapitulated (the coupling constant is defined as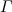 e ² , where is the inverse temperature, and e the counter-ion charge). The opposite limit ( 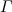∞ is treated by using a recent method based on an exact expansion around the ground-state Wigner crystal of counter-ions. These two limiting results are compared at intermediary values of the coupling constant 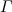= 2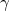 ( 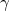= 1, 2, 3) , to exact results derived within a 1D lattice representation of 2D Coulomb systems in terms of anti-commuting field variables. The models (density profile, pressure) are solved exactly for any particles numbers N at 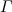= 2 and up to relatively large finite N at 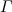= 4 and 6. For the one-line geometry, the decay of the density profile at asymptotic distance from the line undergoes a fundamental change with respect to the mean-field behavior at 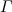= 6 . The like-charge attraction regime, possible for large 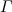but precluded at mean-field level, survives for 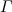= 4 and 6, but disappears at 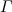= 2 .