https://doi.org/10.1140/epje/i2005-10007-9
Regular Articles
Statistics of ideal randomly branched polymers in a semi-space
1
Physics Department, Moscow State University, 119992, Moscow, Russia
2
LPTMS, Université Paris Sud, 91405, Orsay Cedex, France
3
Landau Institute for Theoretical Physics, 117334, Moscow, Russia
4
A.N. Nesmeyanov Institute of Organoelement Compounds RAS, Vavilova str. 28, 119991, Moscow, Russia
* e-mail: tamm@polly.phys.msu.ru
Received:
28
January
2005
Accepted:
5
April
2005
Published online:
24
May
2005
We investigate the statistical properties of a randomly branched 3-functional N-link polymer chain without excluded volume, whose one point is fixed at the distance d from the impenetrable surface in a 3-dimensional space. Exactly solving the Dyson-type equation for the partition function Z(N, d )= N
-θ
e
γN in 3D, we find the “surface” critical exponent θ =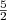 
, as well as the density profiles of 3-functional units and of dead ends. Our approach enables to compute also the pairwise correlation function of a randomly branched polymer in a 3D semi-space.
PACS: 05.40.-a Fluctuation phenomena, random processes, noise, and Brownian motion – / 82.35.Gh Polymers on surfaces; adhesion – / 36.20.Ey Conformation (statistics and dynamics) –
© EDP Sciences, Società Italiana di Fisica and Springer-Verlag, 2005
