https://doi.org/10.1140/epje/s10189-025-00486-3
Regular Article - Flowing Matter
Roughness exponents of the liquid/vapor/solid contact line on surfaces with dilute random Gaussian defects: numerical study
Institute of Mechanics, Bulgarian Academy of Sciences, Academician Georgi Bonchev St. Block 4, 1113, Sofia, Bulgaria
Received:
3
December
2024
Accepted:
28
March
2025
Published online: 16 June 2025
We study here the roughness exponents of the averaged contact line width of a liquid in contact with flat, weakly heterogeneous substrates containing dilute, randomly distributed Gaussian-type defects. For this purpose, we employ the full capillary model. The obtained results for the magnitude of the averaged root-mean-square width of the contact line show that there is only one interval in which the width scales with length as a power function. The numerical studies and analysis indicate that this interval should be regarded as a length scale smaller than the jog length. The roughness exponent found is not a universal constant independent of the apparent contact angle formed by the liquid on the solid surface. It closely approaches the theoretically predicted value of 1/2 [M. O. Robbins, and J. F. Joanny, Europhys. Lett. 3, 729 (1987)] only within the contact angle ranges of 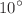 to
to 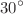 and
and  to
to 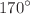 . Furthermore, it can be considered that there is still a significant range of contact angles, from
. Furthermore, it can be considered that there is still a significant range of contact angles, from 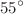 up to
up to 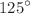 , in which the roughness exponent remains practically constant, however, having a value of 0.8.
, in which the roughness exponent remains practically constant, however, having a value of 0.8.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to EDP Sciences, SIF and Springer-Verlag GmbH Germany, part of Springer Nature 2025
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.




