Eur. Phys. J. E (2025) 48: 11
https://doi.org/10.1140/epje/s10189-025-00476-5

Regular Article – Soft Matter

Macroscopic dynamics of the antiferroelectric smectic $Z_{\text{A}}$ phase and its magnetic analog $Z_{\text{M}}$

¹ Department of Physics, University of Bayreuth, 95440, Bayreuth, Germany
² Max Planck Institute for Polymer Research, 55021, Mainz, Germany

^a pleiner@mailbox.org

Received: 30 September 2024
Accepted: 27 January 2025
Published online: 27 February 2025

Abstract

We analyze the macroscopic dynamics of antiferroelectric smectic $Z_{\text{A}}$ and antiferromagnetic smectic $Z_{\text{M}}$ liquid crystals. The smectic $Z_{\text{A}}$ phase is characterized by antiferroelectric order in one direction in the planes of the smectic layers giving rise to an orthogonal biaxial overall symmetry without polar direction. Thus in sufficiently thick (bulk) samples without externally applied electric fields, globally $D_{2h}$ symmetry results. Therefore, the macroscopic dynamics of the smectic $Z_{\text{A}}$ is isomorphic to that of the McMillan phase and one can take over the corresponding results in the field-free limit. This also applies to the defect structure in the sense that one can expect the appearance of half-integer defects as they have also been observed for the McMillan phase. Based on the fact that ferromagnetic nematic liquid crystals are known for about a decade, it seems natural to investigate the antiferromagnetic analog of the smectic $Z_{\text{A}}$ phase, which we denote as $Z_{\text{M}}$ in the present paper. In this phase, one also has an in-plane preferred direction, which is, however, not like a director in an ordinary nematic, but odd under time reversal. It can be characterized by a staggered magnetization, $\mathit{N}$, just as in a solid antiferromagnet like MnO. As additional macroscopic variables when compared to a usual non-polar smectic A phase, we have the in-plane staggered magnetization and the magnetization $\mathit{M}$. 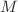As a consequence, we find that spin waves (frequently called anti-magnons in solids) become possible. Therefore, we have for the antiferromagnetic smectic phase, $Z_{\text{M}}$, three pairs of propagating modes: first and ‘second’ sound as in usual smectic A phases and one pair of spin waves. The coupling between ‘second’ sound and spin waves is also analyzed leading to the possibility to excite spin waves by dynamic layer compressions and, vice versa, to generate ‘second’ sound by temporally varying magnetic fields. We note, however, that without additional mechanical or magnetic deformations, the coupling between spin waves on the one hand and first and second sound on the other is a higher order effect in the wave vector $\mathbf{q}$. We also analyze the question of antiferroelectricity and antiferromagnetism for nematic liquid crystals.