https://doi.org/10.1140/epje/s10189-024-00444-5
Regular Article - Flowing Matter
On pressure-driven Poiseuille flow with non-monotonic rheology
CNRS, FAST, Université Paris-Saclay, 91405, Orsay, France
a
laurent.talon@universite-paris-saclay.fr
Received:
25
April
2024
Accepted:
18
July
2024
Published online:
4
August
2024
Shear thickening fluids are liquids that stiffen as the applied stress increases. If many of these types of fluids follow a monotonic rheological curve, some experimental and numerical studies suggest that certain fluids, like cornstarch, may exhibit a non-monotonic, S-shaped rheology. Such non-monotonic behavior has however proved very difficult to observe experimentally in classical rheometer. To explain such difficulties, the possible presence of vorticity banding in the rheometer has been considered. To prevent such instabilities, we use a capillary rheometer, which is a cylindrical tube, measuring the flow rate versus the applied pressure drop. With this setup, we indeed observe a non-monotonic behavior: the flow rate increases monotonically at low pressure drops up to a maximum, after which it abruptly decreases to an almost constant flow rate regardless of further increases in pressure drop. This maximum-jump–plateau behavior occurs over a wide range of concentrations and is reproducible without hysteresis, which is in agreement with an S-shaped rheology. However, the obtained flow versus pressure difference function 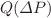 does not agree with the classical Wyart–Cates rheological model, which predicts an S-shaped non-monotonic function, but with neither a jump nor a plateau. To understand this jump–plateau behavior, we remark that any rheological model would establish a relationship between the flow rate and the local pressure gradient, but not the total pressure drop. We thus discuss and analyze the implications of having an S-shaped non-monotonic flow rate-pressure gradient in Poiseuille flow. In particular, we discuss the possibility of a non-uniform pressure gradient in the direction of the flow, i.e., a kind of streamwise banding. The key issue is then the selection of the gradient pressure distribution along the tube. One solution could arise from an analogy of this problem with the spinodal decomposition. It, however, leads to an increase in flow rate with
does not agree with the classical Wyart–Cates rheological model, which predicts an S-shaped non-monotonic function, but with neither a jump nor a plateau. To understand this jump–plateau behavior, we remark that any rheological model would establish a relationship between the flow rate and the local pressure gradient, but not the total pressure drop. We thus discuss and analyze the implications of having an S-shaped non-monotonic flow rate-pressure gradient in Poiseuille flow. In particular, we discuss the possibility of a non-uniform pressure gradient in the direction of the flow, i.e., a kind of streamwise banding. The key issue is then the selection of the gradient pressure distribution along the tube. One solution could arise from an analogy of this problem with the spinodal decomposition. It, however, leads to an increase in flow rate with  up to a plateau between two values of
up to a plateau between two values of  as determined by the Maxwell construction. To account for the bump–jump behavior, we have implemented a simple dynamical stochastic version of the Wyart–Cates model, where the thickening occurs with a characteristic time. As a result, with increasing the total pressure drop, the flow rate increases monotonically up to a maximum value. Beyond this point, the flow rate drops abruptly to a lower value, forming a slowly decreasing plateau. This behavior is likely to account for the maximum-jump–plateau observed in the experiments. We also show that in such a system, the final state is quite sensitive to the initial state of the fluid, especially its homogeneity. Our results then demonstrate that the mere presence of a non-monotonic rheological curve is sufficient to predict the occurrence of stress banding in the streamwise direction and a plateau flow rate, even if the suspension remains homogeneous.
as determined by the Maxwell construction. To account for the bump–jump behavior, we have implemented a simple dynamical stochastic version of the Wyart–Cates model, where the thickening occurs with a characteristic time. As a result, with increasing the total pressure drop, the flow rate increases monotonically up to a maximum value. Beyond this point, the flow rate drops abruptly to a lower value, forming a slowly decreasing plateau. This behavior is likely to account for the maximum-jump–plateau observed in the experiments. We also show that in such a system, the final state is quite sensitive to the initial state of the fluid, especially its homogeneity. Our results then demonstrate that the mere presence of a non-monotonic rheological curve is sufficient to predict the occurrence of stress banding in the streamwise direction and a plateau flow rate, even if the suspension remains homogeneous.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© The Author(s), under exclusive licence to EDP Sciences, SIF and Springer-Verlag GmbH Germany, part of Springer Nature 2024. Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.





