https://doi.org/10.1140/epje/s10189-023-00400-9
Regular Article - Soft Matter
Dynamic structure factor of undulating vesicles: finite-size and spherical geometry effects with application to neutron spin echo experiments
1
Avram and Stella Goldstein-Goren Department of Biotechnology Engineering, and Ilse Katz Institute for Nanoscale Science and Technology, Ben-Gurion University of the Negev, 84105, Beer Sheva, Israel
2
Institut Laue-Langevin (ILL), 71 Avenue des Martys, 38042, Grenoble, CEDEX 9, France
3
Center for Neutron Research, National Institute of Standards and Technology, 100 Bureau Drive, 20899, Gaithersburg, MD, USA
4
Department of Materials Science and Engineering, University of Maryland, 20742, College Park, MD, USA
5
Department of Physics and Astronomy, University of Delaware, 19716, Newark, DE, USA
6
Department of Engineering Sciences and Applied Mathematics, Northwestern University, 60208, Evanston, IL, USA
7
Department of Physics, University of Toronto, 60 St George St, M5S 1A7, Toronto, ON, Canada
a
rgranek@bgu.ac.il
b
hoffmann@ill.fr
c
egk@nist.gov
Received:
20
October
2023
Accepted:
11
December
2023
Published online:
14
February
2024
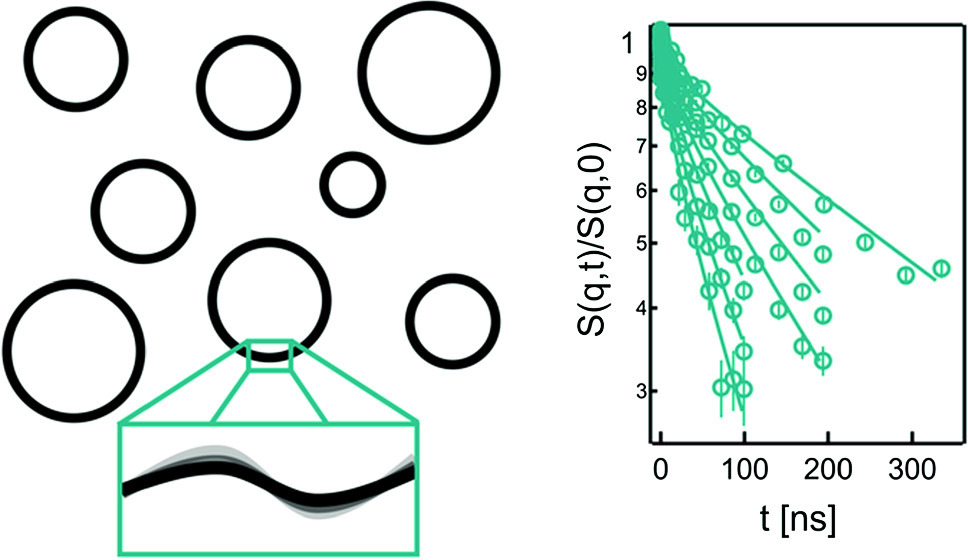
We consider the dynamic structure factor (DSF) of quasi-spherical vesicles and present a generalization of an expression that was originally formulated by Zilman and Granek (ZG) for scattering from isotropically oriented quasi-flat membrane plaquettes. The expression is obtained in the form of a multi-dimensional integral over the undulating membrane surface. The new expression reduces to the original stretched exponential form in the limit of sufficiently large vesicles, i.e., in the micron range or larger. For much smaller unilamellar vesicles, deviations from the asymptotic, stretched exponential equation are noticeable even if one assumes that the Seifert-Langer leaflet density mode is completely relaxed and membrane viscosity is neglected. To avoid the need for an exhaustive numerical integration while fitting to neutron spin echo (NSE) data, we provide a useful approximation for polydisperse systems that tests well against the numerical integration of the complete expression. To validate the new expression, we performed NSE experiments on variable-size vesicles made of a POPC/POPS lipid mixture and demonstrate an advantage over the original stretched exponential form or other manipulations of the original ZG expression that have been deployed over the years to fit the NSE data. In particular, values of the membrane bending rigidity extracted from the NSE data using the new approximations were insensitive to the vesicle radii and scattering wavenumber and compared very well with expected values of the effective bending modulus (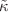
) calculated from results in the literature. Moreover, the generalized scattering theory presented here for an undulating quasi-spherical shell can be easily extended to other models for the membrane undulation dynamics beyond the Helfrich Hamiltonian and thereby provides the foundation for the study of the nanoscale dynamics in more complex and biologically relevant model membrane systems.
This article is dedicated to Fyl Pincus whose pioneering achievements, inspiring approach, and revolutionary ideas in soft condensed matter and biological physics have had a great impact on the entire community in general, and especially on the present authors, including on RG, EGK, MN, and AZ.
Supplementary Information The online version contains supplementary material available at https://doi.org/10.1140/epje/s10189-023-00400-9.
Copyright comment Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
© EDP Sciences, SIF and Springer-Verlag GmbH Germany, part of Springer Nature 2024. Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
