Eur. Phys. J. E (2020) 43: 53
https://doi.org/10.1140/epje/i2020-11979-2

Regular Article

Survival probability of a lazy prey on lattices and complex networks

Department of Physical Sciences, Indian Institute of Science Education and Research Kolkata, 741246, Mohanpur, West Bengal, India

^* e-mail: pprasanta@iiserkol.ac.in

Received: 31 March 2020
Accepted: 15 July 2020
Published online: 14 August 2020

Abstract

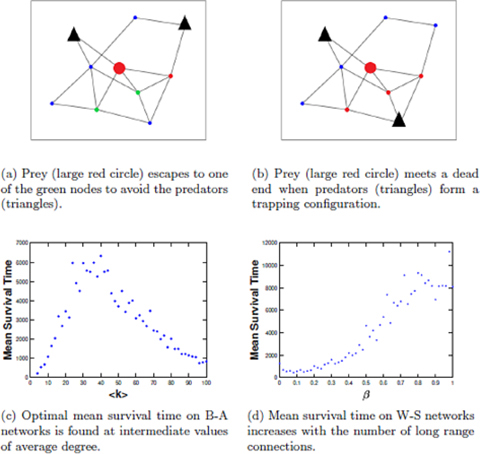
We develop a framework to analyse the survival probability of a prey following a minimal effort evasion strategy, that is being chased by N predators on finite lattices or complex networks. The predators independently perform random walks if the prey is not within their sighting radius, whereas, the prey only moves when a predator moves onto a node within its sighting radius. We verify the proposed framework on three different finite lattices with periodic boundaries through numerical simulations and find that the survival probability (P _sur) decays exponentially with a decay rate proportional to P(N, k) (number of permutations), where k is the minimum number of predators required to capture a prey. We then extend the framework onto complex networks and verify its robustness on the networks generated by the Watts-Strogatz (W-S), Barabási-Albert (B-A) models and a few real-world networks. Our analysis predicts that, for the considered lattices, P _sur reduces as the degree of the nodes of the lattice is increased. However, for networks, P _sur initially increases with the average degree of the nodes, reaches a maximum, and then decreases. Furthermore, we analyse the effect of the long-range connections in networks on P _sur in W-S networks. The proposed framework enables one to study the survival probability of such a prey being hunted by multiple predators on any given structure.