Analytical and numerical stability analysis of Soret-driven convection in a horizontal porous layer: The effect of vertical vibrations

Soumaya Ouadhani; Ali Abdennadher; Abdelkader Mojtabi

doi:10.1140/epje/i2017-11527-3

2024 Impact factor 2.2

Soft Matter and Biological Physics

Non-isothermal transport in complex fluids

Eur. Phys. J. E (2017) 40: 38
https://doi.org/10.1140/epje/i2017-11527-3

Regular Article

Analytical and numerical stability analysis of Soret-driven convection in a horizontal porous layer: The effect of vertical vibrations

Soumaya Ouadhani¹^,2, Ali Abdennadher² and Abdelkader Mojtabi¹^*

¹ IMFT, UMR CNRS/INP/UPS No. 5502, UFR MIG, Paul Sabatier University, 118 Narbonne street, 31062, Toulouse cedex, France
² Carthage University, LIM Laboratory, Polytechnic School of Tunisia, BP 743, 2078, Marsa, Tunisia

^* e-mail: mojtabi@imft.fr

Received: 30 September 2016
Accepted: 9 March 2017
Published online: 5 April 2017

Abstract

The authors studied the effect of vertical high-frequency and small-amplitude vibrations on the separation of a binary mixture saturating a porous cavity. The horizontal bottom plate was submitted to constant uniform heat flux and the top one was maintained at constant temperature while no mass flux was imposed. The influence of vertical vibrations on the onset of convection and on the stability of the unicellular flow was investigated for positive separation ratio 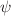$\psi$ . The case of high-frequency and small-amplitude vibrations was considered so that a formulation using time averaged equations could be used. For an infinite horizontal porous layer, the equilibrium solution was found to lose its stability via a stationary bifurcation leading to unicellular flow or multicellular one depending on the value of 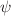$\psi$ . The analytical solution of the unicellular flow was obtained and separation was expressed in terms of Lewis number, separation ratio and thermal Rayleigh number. The direct numerical simulations using the averaged governing equations and analytical stability analysis showed that the unicellular flow loses its stability via oscillatory bifurcation. The vibrations decrease the value of 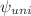$\psi_{uni}$ , which allows species separation for a wide variety of binary mixtures. The vibrations can be used to maintain the unicellular flow and allow species separation over a wider range of Rayleigh numbers. The results of direct numerical simulations and analytical model are in good agreement.