Eur. Phys. J. E (2015) 38: 76
https://doi.org/10.1140/epje/i2015-15076-5

Regular Article

Moving line model and avalanche statistics of Bingham fluid flow in porous media

CNRS, Laboratoire FAST, UMR 7608, Université Paris-Sud, F-91405, Orsay, France

^* e-mail: chevalier@fast.u-psud.fr

Received: 26 February 2015
Revised: 27 May 2015
Accepted: 9 June 2015
Published online: 15 July 2015

Abstract

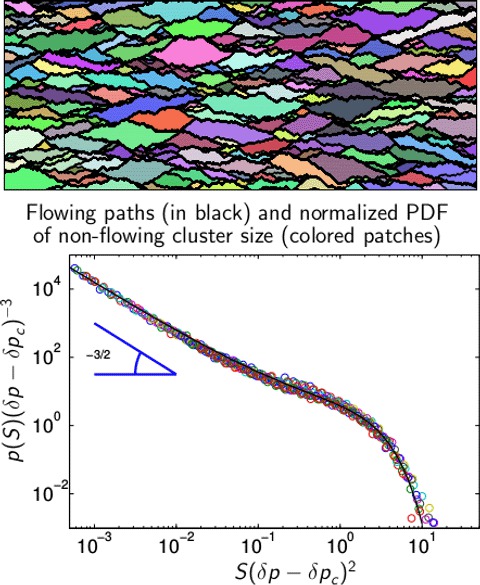
In this article, we propose a simple model to understand the critical behavior of path opening during flow of a yield stress fluid in porous media as numerically observed by Chevalier and Talon (2015). This model can be mapped to the problem of a contact line moving in an heterogeneous field. Close to the critical point, this line presents an avalanche dynamic where the front advances by a succession of waiting time and large burst events. These burst events are then related to the non-flowing (i.e. unyielded) areas. Remarkably, the statistics of these areas reproduce the same properties as in the direct numerical simulations. Furthermore, even if our exponents seem to be close to the mean field universal exponents, we report an unusual bump in the distribution which depends on the disorder. Finally, we identify a scaling invariance of the cluster spatial shape that is well fit, to first order, by a self-affine parabola.