Eur. Phys. J. E (2009) 29: 107-115
https://doi.org/10.1140/epje/i2009-10454-2

Regular Article

Finite- N effects for ideal polymer chains near a flat impenetrable wall

Department of Mathematics, University of Reading, Reading RG6 6AX, Whiteknights, UK

^* e-mail: m.w.matsen@reading.ac.uk

Received: 5 March 2009
Accepted: 25 March 2009
Published online: 14 May 2009

Abstract

This paper addresses the statistical mechanics of ideal polymer chains next to a hard wall. The principal quantity of interest, from which all monomer densities can be calculated, is the partition function, G _N(z) , for a chain of N discrete monomers with one end fixed a distance z from the wall. It is well accepted that in the limit of infinite N , G _N(z) satisfies the diffusion equation with the Dirichlet boundary condition, G _N(0) = 0 , unless the wall possesses a sufficient attraction, in which case the Robin boundary condition, G _N(0) = - 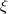G _N ^′(0) , applies with a positive coefficient, 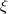. Here we investigate the leading N ^-1/2 correction, 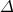G _N(z) . 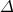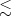Prior to the adsorption threshold, G _N(z) is found to involve two distinct parts: a Gaussian correction (for z aN ^1/2 with a model-dependent amplitude, A , and a proximal-layer correction (for z 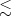a described by a model-dependent function, B(z) .