Eur. Phys. J. E 5, 575-582 (2001)
Helices and helix packings derived from the
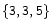polytope
J.F. Sadoc Laboratoire de Physique des Solides (associé au CNRS) , bâtiment 510, Université de Paris-Sud, 91405 Orsay Cedex, France sadoc@lps.u-psud.fr
(Received 8 March 2001 and Received in final form 25 June 2001)
Abstract
The 
-polytope is described and used as template for dense
structures. Then larger structures are derived from this polytope, using
disclinations. That needs a study of symmetries in this polytope. A
discretised version of the Hopf fibration is presented and used in order to
generate a family of new polytopes. It is possible to gathered vertices of
these structures on several helices and then to consider geometrical
relation between these helices. This study is govern by biological
consideration of helix building molecules,
but the final purpose is to have
a geometrical tool to study geometrical relationship
occurring between different helices or strands. This
can occur for instance in protein folding studies.
87.10.+e - General, theoretical and mathematical biophysics.
36.20.-r - Macromolecules and polymer molecules.
© EDP Sciences, Società Italiana di Fisica, Springer-Verlag 2001
